
Définition :
Une flèche est la distance entre une surface et un plan tangent à cette surface. Il est courant en lunetterie de définir les surfaces optiques par une liste de flèches données à différents angles et différentes distances d’un point de référence. On définie alors les surfaces dans un repère cylindrique (r, a, z) où r est la distance au point de référence, a est l’angle d’orientation et z la flèche.

On utilise beaucoup les flèches pour calculer le rayon de courbure des surfaces qui sont générées à partir de cercles (surfaces sphériques ou surfaces toriques), car on peut facilement mesurer la flèche sur ce type de surface (avec un sphéromètre ou un torimètre) et en déduire le rayon de courbure par calcul. Il existe en effet une relation simple entre le rayon de courbure et la flèche.
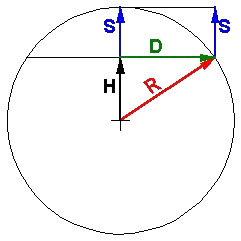
Soit un cercle de rayon R et la flèche S mesurée à une distance D. Dans le triangle définit par les vecteurs H, D et R on a :
R² = H² + D²
or H = R – S
donc R² = (R – S)² + D²
En développant cette équation, on obtient les deux relations :
et
Exemple :
Un rayon de courbure R = 100 mm sur un demi-diamètre D = 20 mm donne une flèche :
S = 100 – Racine(100² – 20²) = 2.02 mm.
On peut vérifier le calcul inverse et retrouver le rayon à partir de la flèche.

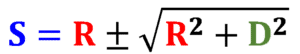
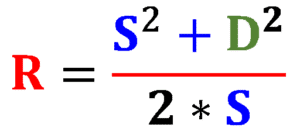
Il faut corriger la première relation déduite en mettant un – à la place du + dans la racine :
S = R – Racine(R² – D²)
Comme le montre l’exemple
Bonjour Michel, Je vous remercie pour votre retour, effectivement, la formule comporte une erreur de signe, mais l’application numérique est correcte. Nous corrigeons dans les plus brefs délais.
Cordialement