
Définition :
Puissance et astigmatisme régulier :
Pour comprendre le principe de l’abérrométrie, il faut d’abord rappeler quelques éléments de base :
La puissance dioptrique est une variation régulière de l’effet prismatique sur une portion de surface, faisant diverger ou converger les rayons lumineux de ou vers un point. Dans un verre de lunettes, le prisme varie entre le centre et le bord.
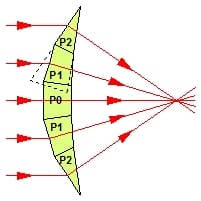
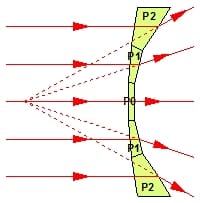
Un frontofocomètre mesure la puissance d’un verre sur une surface de 6 à 8 mm de diamètre (6mm pour un verre de contact). Si on réduisait ce diamètre on réduirait la variation prismatique entre le centre et le bord de la surface analysée et donc la précision de l’appareil. On peut facilement mettre ce phénomène en évidence sur un frontofocomètre manuel à réticule, en réduisant fortement le diamètre du faisceau lumineux de sortie, la mire paraît alors toujours nette sur une grande plage de puissance, on ne peut donc plus déterminer précisément la puissance du verre. A l’extrême, si on réduit la surface analysée à un point, il ne passerait plus qu’un seul rayon lumineux et on n’obtiendrait pas une puissance mais simplement l’effet prismatique en ce point. A l’inverse, si on agrandissait le diamètre de mesure, on ne pourrait plus mesurer les verres progressifs car on intégrerait dans la mesure la variation de puissance de la surface progressive et la mesure obtenue ne correspondrait à rien.
Lorsque l’on parle de la puissance d’une surface, on considère que cette surface doit être parfaitement soit sphérique soit torique (ou encore cylindrique ou plane) et qu’elle est donc générée par des cercles avec au plus, deux méridiens principaux perpendiculaires l’un à l’autre. Tout autre type de surface ne peut définir une puissance. Pour s’en convaincre, il suffit d’essayer de mesurer au frontofocomètre la puissance d’un verre progressif en dehors des zones stabilisées (vision de loin, vision intermédiaire ou vision de près), on obtient généralement du fronto un message d’erreur du style « erreur de mesure » ou « surface irrégulière » et sur un fronto manuel à réticule, il est impossible d’obtenir une image nette du réticule. On ne peut donc mesurer que des puissances sphériques ou des astigmatismes réguliers (sous la forme d’une sphère et d’un cylindre).
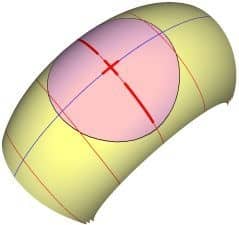
Le Tore génère un astigmatisme régulier
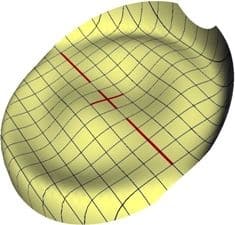
Exemple de surface générant un astigmatisme irrégulier non mesurable au frontofocomètre
L’abérrométrie a pour but de mesurer et quantifier l’ensemble des aberrations de l’œil. Le principe consiste à envoyer dans l’œil un front d’onde plan, correspondant à un faisceau de rayons parallèles provenant de l’infini. Dans un œil parfait, ce faisceau vient converger sur la rétine puis est réfléchie et ressort par la cornée sous la forme d’un front d’onde plan F comme le montre l’animation ci-dessous.
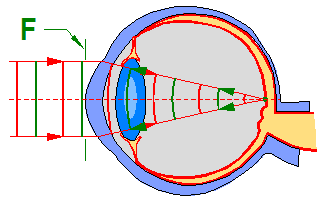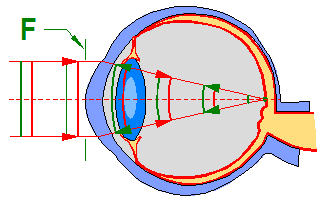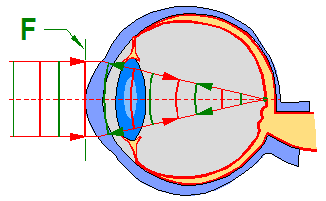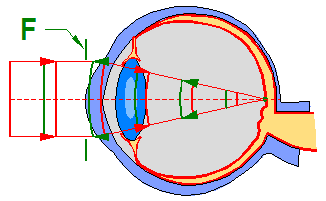
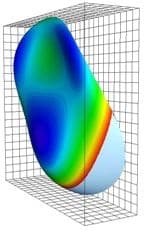
Il est important de noter que la forme du front d’onde peut varier beaucoup en fonction du diamètre d’ouverture de la pupille. Plus la pupille est ouverte (en vision nocturne par exemple), plus on a de chance de voir apparaître des aberrations de haut degré.

Certains appareils comme celui ci-contre, sont aussi capables de faire une mesure de la topographie cornéenne sachant qu’une grande partie des aberrations sont dues à des déformations de la cornée.
Analyse de la mesure du front d’onde :
Une fois le front d’onde mesuré, reste à savoir comment l’interpréter. Pour y parvenir, on va décomposer la surface du front d’onde en une somme de surfaces élémentaires qui vont correspondre à des aberrations élémentaires connues (défocalisation, cylindre, trefoil, coma,…). On va ensuite pouvoir quantifier chacune de ces aberrations grâce aux facteurs de Zernike.
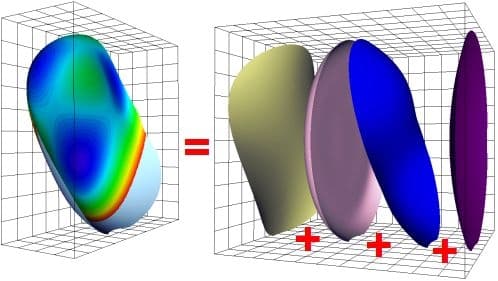
Ici le front d’onde analysé est la somme (de gauche à droite)
d’un Trefoil + Aberration sphérique + Coma + Défocus
Polynômes de Zernike :
Les polynômes de Zernike sont un ensemble de fonctions mathématiques polynomiales permettant de décomposer des surfaces complexes en une somme infinie de surfaces élémentaires. Ces fonctions sont très souvent utilisées en optique pour analyser les fronts d’ondes. Ces fonctions sont notées :

Où m est l’indice de fréquence angulaire et n est le degré du polynôme.
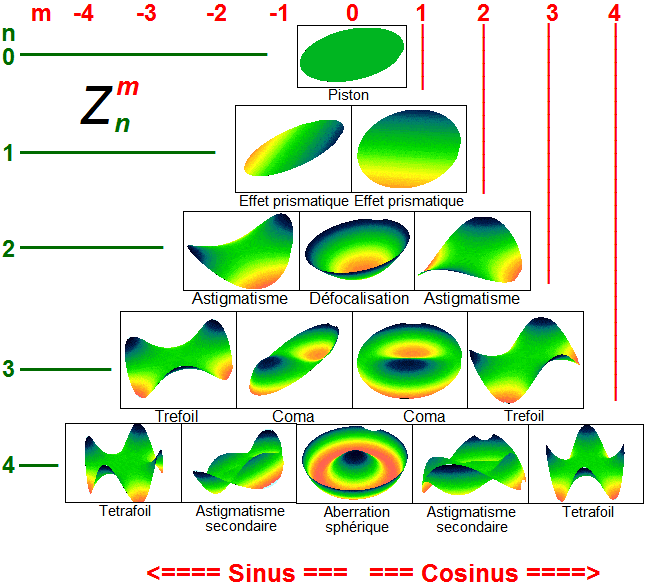
On remarque que pour chaque degré, il existe les mêmes surfaces à droite et à gauche. Les surfaces du coté droit (avec m positif) sont tournées de 90° par rapport à leur symétrique de gauche (m négatif). En combinant ces deux surfaces, on peut obtenir le même type de surface mais avec n’importe quelle orientation.
Lorsque le degré n est pair, la fréquence angulaire m est aussi paire.
Degré 0 : Appelé « Piston », ce degré ne correspond qu’à un décalage et n’a pas de conséquence sur la vision.
Degré 1 : Ces 2 aberrations correspondent à des anomalies de centrage et n’affectent généralement pas la capacité visuelle.
Degré 2 : Ce degré correspond aux amétropies bien connues en lunetterie (myopie, hypermétropie et astigmatisme).
Degré 3 : C’est le début des aberrations de haut degré. Il s’agit ici du Trefoil et de la Coma.
Degré 4 : Il correspond au Tétrafoil (ou quadrifoil), l’astigmatisme secondaire et l’Aberration sphérique.
…
Coefficients de Zernike :
Pour représenter un front d’onde quelconque, on le décompose en fonctions de Zernike en donnant à chacune de ces fonctions un poids à l’aide d’un coefficient. Un front d’onde peut donc être représenté par une somme des fonctions de Zernike multipliés par un coefficient sous la forme :
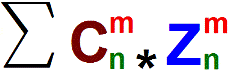
Avec C(n,m) le coefficient pour chaque fonction Z(n,m).
Les fonctions de Zernike Z(n,m) étant parfaitement connues, il suffit de mémoriser les coefficients C(n,m) pour définir l’ensemble des aberrations de l’œil.
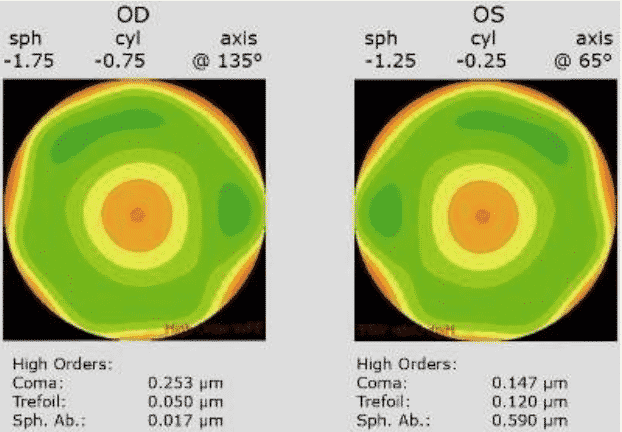
Le tableau ci-dessous montre la décomposition en facteurs de Zernike de la mesure abérrométrique de mon œil droit (il faut savoir donner de sa personne…). On remarque une forte hypermétropie Z(2,0), un fort astigmatisme Z(2,2), un peu de Coma Z(3,1)
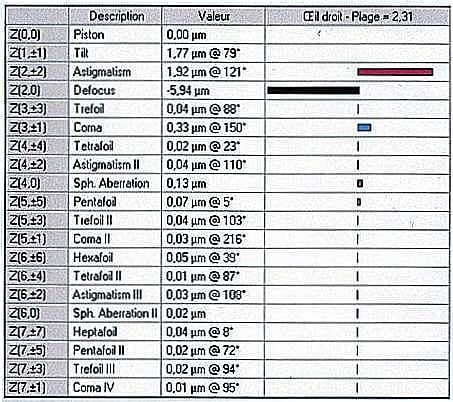
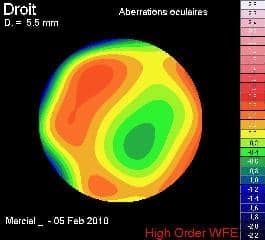
En règle générale, les aberrations de haut degré diminuent pour les facteurs d’ordre élevés sauf pour des cornées très déformées comme dans le cas des kératocônes.
Correction des aberrations :
Il n’est malheureusement pas possible de corriger directement les aberrations de haut degré avec des verres de lunettes car ces aberrations ont toutes un centre de symétrie. La démonstration ci-dessous n’est pas totalement scientifique mais je l’espère assez convaincante.

En conclusion, on remarque qu’un astigmatisme de haut degré (supérieur à 2) ne conserve pas ses propriétés optiques lorsque l’on s’éloigne de son centre de symétrie. Voilà pourquoi on ne peut pas corriger directement ce type d’astigmatisme avec un verre de lunette car il faudrait que l’œil reste parfaitement immobile face à ce centre de symétrie. Les aberrations sphéro-toriques (aberrations d’ordre 2) Z(2,0) et Z(2,2) ne présentent pas cet inconvénient car elles ont un méridien de symétrie.
Cependant, grâce à la technologie Freeform, certains verriers utilisent les mesures abérrométriques pour améliorer le calcul des surfaces à usiner, en introduisant des compensations sphéro-toriques pour compenser partiellement ces aberrations de haut degré. Nous sommes encore au début de cette technologie et il reste beaucoup de concepts à découvrir qui permettront d’améliorer la vision.
La chirurgie réfractive (PKR, Lasik) prend aussi en compte l’ensemble des aberrations de haut degré mais les effets de la cicatrisation peuvent parfois introduire d’autres aberrations de haut degré (en particulier en vision nocturne où la pupille est grande ouverte).

0 commentaires