Abbe value 

On considère qu’en dessous d’un nombre d’Abbe de 40, l’irisation colorée est perceptible par l’oeil. Malheureusement, en règle générale, plus les matières ont un indice de réfraction élevé (permettant de réaliser des verres plus minces) plus leur nombre d’Abbe faible ; elles ont donc tendance à décomposer la lumière. Le porteur doit donc parfois faire un compromis entre l’esthétique du verre et sa qualité optique. En fait, le chromatisme sera sensible si le nombre d’Abbe est petit, si le rayon lumineux est éloigné de l’axe optique et si la puissance du verre est grande.

Soit :

 u : Le nombre d’abbe du verre
 D : La puissance du verre en dioptries
 d  : Le décentrement en centimètres

Pour que le chromatisme ne soit pas gênant, il faut que :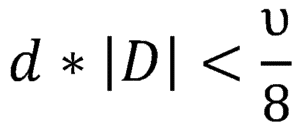

Exemple :

Soit un verre de puissance D = +4.00 de constringence u = 30, le décentrement maximal sans gène chromatique sera

d = u / 8D = 0.93 cm

Quelques valeurs de nombre d’Abbe :

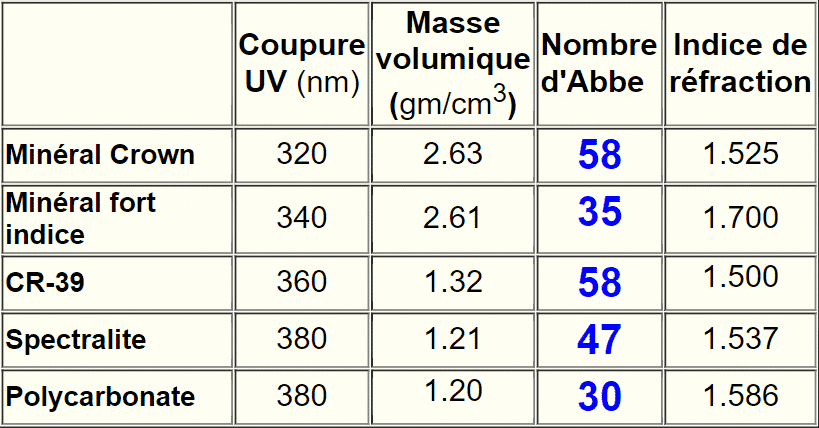
Définition physique :

La constringence correspond en fait à la variation d’indice de réfraction de la matière en fonction de la longueur d’onde (c’est à dire de la couleur) de la lumière. On calcule cette variation d’indice sur les couleurs extrêmes (le rouge et le bleu). Cette variation d’indice fait varier la puissance du verre.

Exemple :

Soit un verre minéral d’indice 1.7 (1.7/35 Corning) dont on mesure l’indice sous plusieurs longueurs d’onde. Ces lumières sont normalisées et obtenues à l’aide de lampes spéciales (la raie e = 546.1 nm est obtenue à l’aide d’une lampe à vapeurs de mercure).

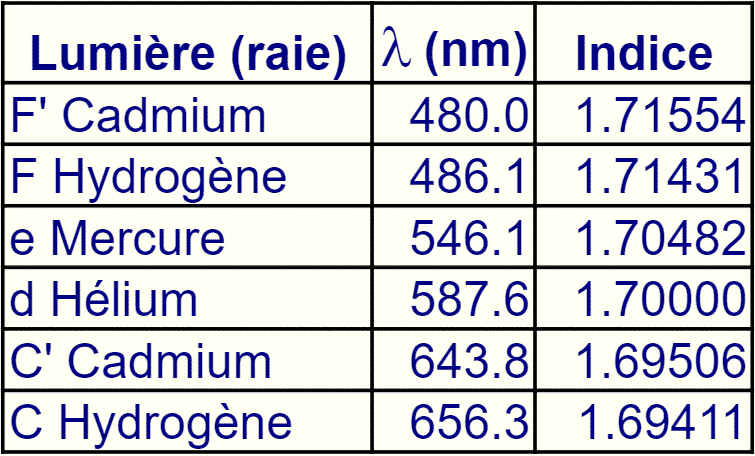
En Europe, on calcule la constringence centrée sur la raie verte (e) d’une lampe à mercure.

            N_e – 1              1.70482 – 1
Ve = ————— = ————————— = 34.4
           N_F’ – N_C’      1.71554 – 1.69506

Aux Etats Unis, on utilise la raie jaune (d) d’une lampe à hélium.

            N_d – 1          1.70000 – 1
Vd = ———— = ———————— = 34.6
         N_F – N_C      1.71431 – 1.69411

Exemple :

• Soit un verre organique normal (en CR39) de +3.00 dioptries. Cette matière ayant une constringence de 58, le verre fera +3.00 +/-3.00/58 soit +3.05 en lumière bleue et +2.95 en lumière rouge.
• Le même verre 3.00 réalisé en matière polycarbonate. Cette matière ayant une constringence de 30, le verre fera +3.00 +/-3.00/30 soit +3.10 en lumière bleue et +2.90 en lumière rouge.

Si le nombre d’Abbe permet de quantifier la variation globale d’indice d’une matière en fonction de la longueur d’onde de la lumière qui la traverse, l’équation de cette variation reste spécifique à chaque matière et il n’est donc malheureusement pas possible de calculer l’indice d’une matière pour n’importe quelle longueur d’onde, à partir de sa constringence.

La formule de Cauchy donne cependant une assez bonne représentation de la variation d’indice n d’une matière en fonction de la longueur d’onde λ par :
n = a + b/λ²

a et b pouvant être calculés à partir de deux indices connus de la matière.

Nota : L’œil a une constringence comprise entre 43 et 45