
Définition :
Unité de mesure de la puissance (vergence) d’un système optique. Cette unité notée δ ou m-1 (inverses de mètres) voir parfois Dpt, correspond à l’inverse de la distance de vergence du système optique.
La puissance qualifie le pouvoir d’un système optique à faire converger ou diverger la lumière (on parle aussi de vergence). L’unité de mesure de puissance est la dioptrie notée δ ou m-1 (inverses de mètres) et correspond à l’inverse de la distance focale f’ du système optique.
f ‘ = SF’ est la distance entre le verre et son point focal F’. Elle est comptée positive dans le sens de la lumière.

A la différence de la distance focale, les dioptries offrent l’avantage de pouvoir s’ajouter. En collant deux verres d’1.00 dioptrie l’un contre l’autre, on obtient l’équivalent d’un verre de 2.00 dioptries (ce qui n’est pas du tout le cas pour les distances focales). La simple somme de dioptries est bien sûr approximative car il faut tenir compte de l’épaisseur au centre du verre.
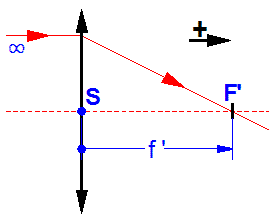
Verre convergent
Considérons des rayons lumineux arrivant parallèlement à l’axe optique d’un verre convexe (verre convergent), ces rayons vont converger au point F’ que l’on appelle : point focal image.
La distance (f’), qui sépare la face concave du verre et le point focal F’ est appelée distance frontale arrière.
En lunetterie, la puissance d’un verre (notée D’f), correspond à l’inverse de cette distance frontale arrière (f’ doit être exprimée en mètres) :
1
D’f = —–
f’
Exemple : Un verre qui fait converger les rayons à f’ = 20cm de sa face arrière (soit 0.2m) a une puissance
1
D’f = —– = +5.00 dioptries.
0.2
Dans le cas d’un verre convexe, la puissance est positive car la distance frontale arrière est compté positive de la surface S au point focal F’.
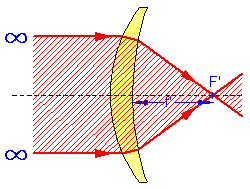
Dans le cas d’un verre convexe, la puissance est positive car la distance frontale arrière est compté positive de la surface S au point focal F’.
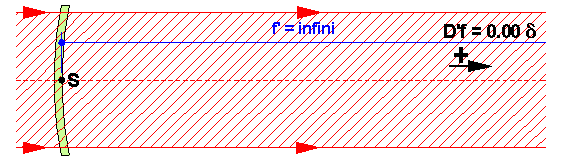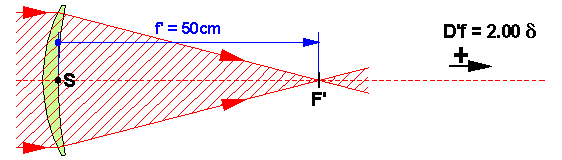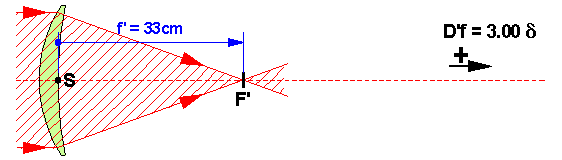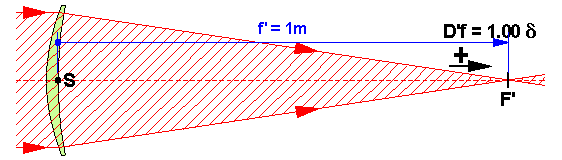
+1.00 dioptrie fait converger la lumière à 1 mètre
+2.00 dioptrie fait converger la lumière à 50cm (1/2 mètre)
+3.00 dioptrie fait converger la lumière à 33.333…cm (1/3 mètre)
+4.00 dioptrie fait converger la lumière à 25cm (1/4 mètre)
0.00 dioptrie (appelé verre PLAN) ne fait ni converger ni diverger la lumière
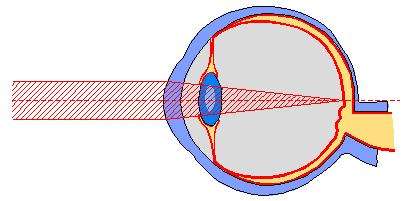
L’oeil fonctionne comme une lentille convergente dont la puissance est d’environ +59.00 dioptries en moyenne.
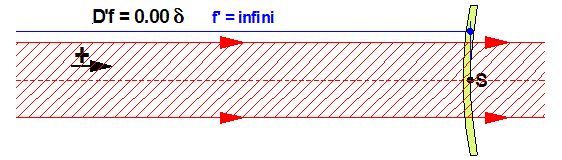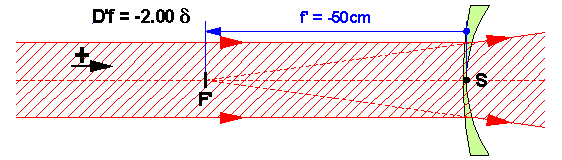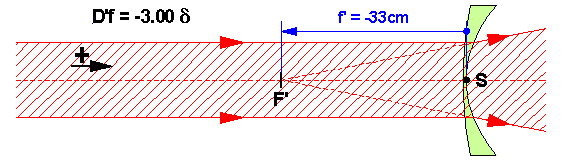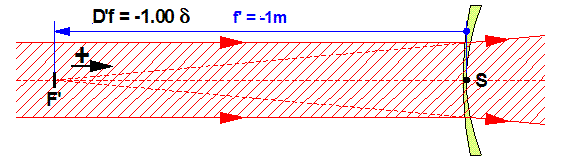
Verre divergent
Dans le cas d’un verre concave (divergent), les rayons lumineux arrivant parallèlement à l’axe optique vont diverger en semblant provenir du point focal image F’ situé en avant du verre (tracé en pointillés). La distance frontale arrière f ‘ étant alors négative (SF’ < 0), notre formule D’f = 1 / f’ donnera une puissance négative.
Exemple : Un verre qui fait diverger les rayons à –80 cm (soit -0.8 m) a une puissance D = 1 / -0.8 = -1.25 δ.

0 commentaires