
Définition :
Appareil utilisé pour mesurer les rayons de courbures des surfaces toriques, basé sur le même principe que le sphéromètre. On mesure la flèche d’appuie et on déduit par calcul le rayon de courbure de la surface.
Le torimètre à bille permet de mesurer avec précision les rayons de courbure d’une surface torique (ou sphérique). Il peut être utilisé pour mesurer les courbures de la surface arrière d’un verre, la base d’un verre ou les courbures d’un outil de surfaçage.
Basé sur le même principe que le sphéromètre, le torimètre mesure la flèche d’appui S sur la surface à mesurer. Il se compose de deux billes fixes de rayon r et d’une bille mobile montée sur un comparateur. On applique les trois billes sur l’un des deux méridiens du tore à mesurer et on lit la flèche (mm) sur le cadran. Cet appareil nécessite une bonne habitude pour obtenir des mesures précises car il faut bien le positionner dans le méridien de la surface (une mesure entre deux méridiens n’ayant aucun intérêt). Pour cela, on tourne le verre (ou l’outil) sous l’appareil jusqu’à ce que l’aiguille du comparateur rebrousse chemin, on est alors soit dans le méridien le plus plat soit méridien le plus cambré.
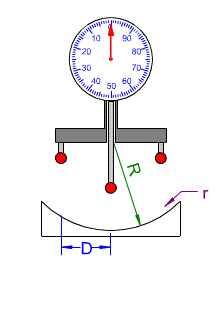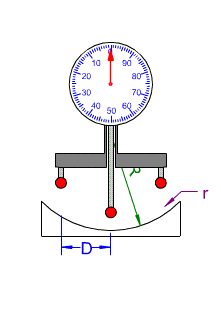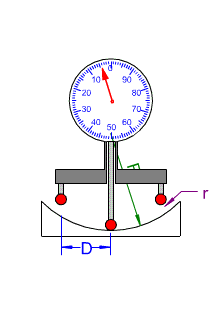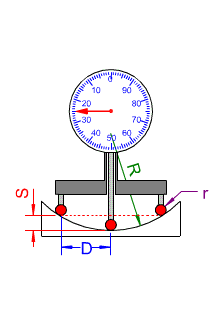
On calcule le rayon de courbure par :
| (S² + D² – 2 * r * S) R = ——————————— (2 * S) |
Pour un même rayon de courbure, l’appareil ne mesure pas exactement la même flèche sur une surface concave ou une surface convexe car le point de contact de la bille sur la surface change à cause du diamètre des billes. La bille touche à l’extérieur sur une surface concave (distance D2) et à l’intérieur sur une surface convexe (distance D1).
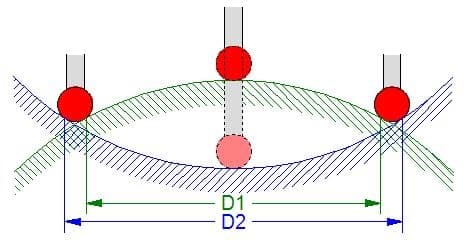
Pour prendre en compte ce phénomène, il faut indiquer dans cette formule, une valeur de flèche S positive pour une surface convexe et négative sur une surface concave.
Exemple :
Soit un torimètre dont les billes ont un rayon r = 1.5mm, dont le demi-entraxe de billes D = 20mm.
Si on mesure une flèche S = 2.5mm, on obtient le rayon de courbure R de la surface par :
– Sur une surface convexe R = (20² + 2.5² – 2 * 1.5 * 2.5) / (2 * 2.5) = 79.75mm
– Sur une surface concave R = (20² + (-2.5)² – 2 * 1.5 * –2.5) / (2 * –2.5) = -82.75mm
Noter que sur une surface concave, on obtient un rayon de courbure négatif mais ce n’est qu’une question de convention.
A l’inverse, on peut calculer la flèche torique S correspondant à un rayon R par :
|
S = R + r – Racine((R + r)² – D²) pour une surface convexe |
Ces appareils sont fournis avec des abaques indiquant la correspondance entre chaque valeur de flèche et la puissance correspondante en Dioptries (souvent pour un indice 1.523). L’abaque des mesures de surface concave est bien sûr différent de celui des surfaces convexes.
Plus la distance entre les billes est grande, plus l’appareil est précis. On trouve communément des appareils avec un entraxe de billes de 40mm (D=20) et plus rarement avec un entraxe de 50mm (D=25). Le diamètre des billes est souvent de 3 mm (r = 1.5)

0 commentaires